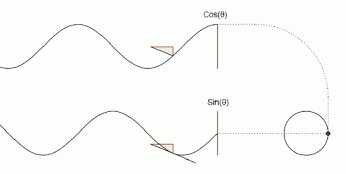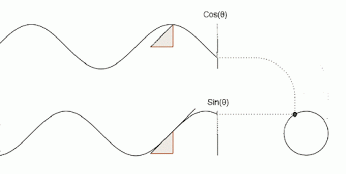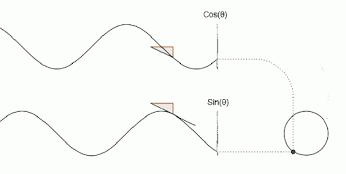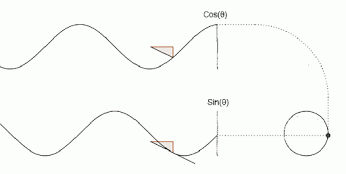
x(t) = Cos(t)

y(t) = Sin(t)

To find the unit vector, you divide the vector by its magnitude. 

Tangent vectors are relatively simple. On a curve, a tangent vector is a vector that lies on the tangent line at a point. For those who don’t know, a tangent line is a straight line that follows the slope at a singular point on a curve. 

In physics, one use of vectors is in a position function, which plots an object's position in terms of time. When you enter 2D or 3D space, you need vectors to accurately represent the object's location. In 2D, this is represented as 

P(t) = (x(t), y(t))

where x(t) and y(t) are the x and y functions for the position. This idea of using time and multiple dimensions for one function is known as parameterization. In this case, t is our parameter. A common parametric function is:

As t increases, the corresponding x and y functions are plotted together to create a circle. 

Physicists use the position function, P(t), to find other data about the object, such as its velocity, or change in position per time, which can be found with the derivative of P(t), or P’(t).

V(t) = (x’(t), y’(t))

Velocity and speed are not the same. Despite having the same magnitude, the velocity has direction, while speed does not, meaning it will always be positive. This is why when you’re reversing in your car, the speedometer still shows a positive value. 

Furthermore, this process can be used again to find the acceleration or change in velocity per time, of that same position function. After acceleration comes jerk, or change in acceleration per time. Interestingly enough, the next 3 derivatives are snap, crackle, and pop.